
EPFLSTILOBMarcel LeuteneggerAbout
MATLAB toolbox
Double class
 |
EPFLSTILOBMarcel LeuteneggerAbout MATLAB toolbox Double class |
|---|
MATLAB toolbox
Double class
Extended class
Single class
Flex99-12C correlator
Flex02-0xD correlator
Vector functions
MEX-Builder
I regularily deal with a huge number of elementary functions as rounding, transcendentals, exponential and logarithm and was unsatisfied with the average performance. So, I started to provide my own assembler subroutines executing with full floating-point performance on any Intel Pentium II+ or compatible system. On recent Pentium 4 computers, I was able to improve the average performance by two to five times.
This archive is dedicated to any number cruncher using MATLAB 6.0 or newer.
Unpack the folder '@double' from the archive.
builtin(func,arguments) to call the original version of func. Please note that this works only for built-in functions - this means that which func reports "func is a built-in function".func into ffunc. Existing MATLAB code will work with the built-in functions unless you call ffunc.If you work with MATLAB R13 or newer, you may replace 'xor.dll' by 'xur.dll' for matching the representation of logical values (uint8).
The libraries should always reside in a subfolder called '@double' to make sure they are not called for any data except of type double. They do not check the data type of passed arguments.
Due to the overhead for calling external functions, the built-in functions work faster if called for matrices with less than about 4 to 8 elements. Therefore, if you know the size of your matrix, you can choose the appropriate function.
The functions angle, mod and xor are not built-in but MATLAB scripts. Therefore, the functions within this package work much faster in any case as shown in the following figure.
The function xur is an even faster version of xor. It can be used in any situation where its output, a logical (boolean) uint8 matrix, will not be transformed to double for computation. It serves in particular as a value selector in a statement like values=matrix(xur(a,b)).
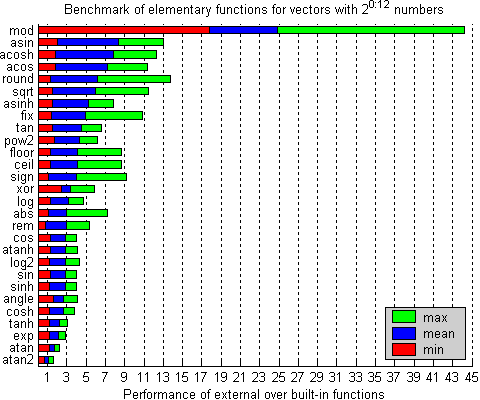
Figure 1: Benchmark on a 2GHz Pentium 4 Mobile system
The results of the external functions slightly differ from the built-in functions. The accuracy of the external functions benefits from the floating-point registers with a 64bit mantissa on Intel processors. Intermediate values are kept in floating-point registers such that rounding takes place mostly once - when writing the result into the output matrix with a 53bit mantissa.
In general, a statement of inverseFunction(function(value)) produces value with a relative error of less than 1.0E-13. The roundoff error of about 1.1E-16 leads to relatively important deviations in exponentiation. Note also that in particular addition/subtraction in the argument of a logarithm are critical operations due to a relative amplification of the rounding error. The logarithm itself works accurate over the full complex plane R x iR. For the sake of performance, the inverse transcendental functions are currently not implemented in that way. See also the summary about complex functions.
An exception is made for every periodic transcendental function, where the constant 2pi is truncated to a 53bit mantissa. This guarantees that a statement of the form sin(x) with real x always produces the expected value sin(rem(x,2*pi)) at the same accuracy. The reminder is computed explicitly and prescaled to a 64bit mantissa.
Example 1:
x=pow2(pi,0:256);
plot(x,builtin('sin',x),'r',x,sin(x),'b');
set(gca,'XScale','log');Copyright © Marcel Leutenegger, 2003-2007, École Polytechnique Fédérale de Lausanne (EPFL),
Laboratoire d'Optique Biomédicale (LOB), BM - Station 17, 1015 Lausanne, Switzerland.
This library is free software; you can redistribute it and/or modify it under
the terms of the GNU Lesser General Public License as published by the Free
Software Foundation; version 2.1 of the License.
This library is distributed in the hope that it will be useful, but WITHOUT ANY
WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A
PARTICULAR PURPOSE. See the GNU Lesser General Public License for more details.
You should have received a copy of the GNU Lesser General Public License along
with this library; if not, write to the Free Software Foundation, Inc.,
51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA.
See '/FILES' in the source archive for a list of the original package contents.
Any warranty is strictly refused. Don't rely on any financial or technical support in case of malfunction or damage.
Comments are welcome. I will try to track reported problems and fix bugs.
Initial release
Bug fixed in rem(matrix,value): the result was stored back to the value causing an assertion failure.
Service release thanks to a bug reported by Tom Minka in exp(matrix): the output was NaN for infinite input.
This bug fix made me think about affine inputs. They are now all handled as particular values for two reasons:
Service release. Bux fixed in [c,s]=cis(matrix): the second output was set to an invalid dimension. Version information included.
Source code released under GNU Lesser General Public License (LGPL) version 2.1.
Optimized routine for calculating the exponential according to Agner Fog, "Optimizing subroutines in assembly language," at Copenhagen University College of Engineering.
Dimensions of (empty matrix*scalar) matched on MATLAB's behaviour. Thanks to Paolo Bardella for reporting the issue.
Bug report by Tom Minka: with MATLAB 7, the double functions are also called for sparse input returning a broken output. As a workaround, you may rename the functions or include/exclude them in/from the MATLAB path.
Dimensions of function(empty matrix,scalar) do not match with MATLAB's behaviour.
Downloading these files, you accept the copyright terms.
MATLAB is a registered trademark of The MathWorks, Inc. Pentium II is a registered trademark of Intel Corporation. Other product or brand names are trademarks or registered trademarks of their respective holders.
© 2011 École Polytechnique Fédérale de Lausanne