• Introduction
• Requirements
• Compatibility
• Comments
• Copyright
• Warranty
• History
• Download
• Trademarks

Introduction

This package contains binaries of a Linux port of Marcel Leutenegger's performance enhanced elementary MATLAB functions. Since these functions are implemented in architecture specific assembly language, they only work on x86-based Linux systems. Thanks to MATLAB's mostly platform independent way of dealing with MEX functions, these primitives can and should be installed and used in the way that is described in double class.

Requirements

• An x86-based Linux system with an Intel Pentium II or better processor.
• MATLAB R13 build 6.5.0.180913a or newer.

Compatibility

These functions have been compiled using GCC version 3.3.2 on a GLIBC 2.3 based system. I sucessfully tested their functionality on a recent Debian (testing) and a recent Gentoo (2004.0) system (recent as of 3/5/2004). However, I know that certain binaries that were compiled on GLIBC 2.3 based systems do not run on systems with older versions of this library. Since I don't have access to any such Linux system, I cannot verify whether this is the case for the MEX functions provided here.

Comments

The libraries should always reside in a subfolder called '@double' to make sure they are not called for any data except of type double. They do not check the data type of passed arguments.

Due to the overhead for calling external functions, the built-in functions work faster if called for matrices with less than about 4 to 8 elements. Therefore, if you know the size of your matrix, you can choose the appropriate function.

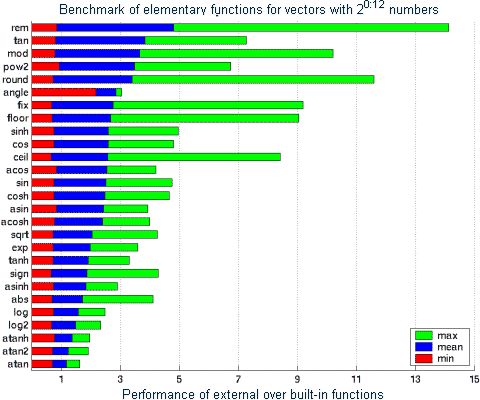
Figure 1: Benchmark on a recent Linux distribution

Copyright

These routines are published in terms of freeware. The author reserves the right to modify any of the routines listed below.

You are allowed to distribute this package as long as you deliver the entire, original package for free.

Path		File		Description
/		Linux.txt		Linux specific information
		Readme.txt		This manual
@double/		abs.mexglx		Absolute value
		acos.mexglx		Inverse cosine
		acosh.mexglx		Inverse hyperbolic cosine
		angle.mexglx		Phase angle of complex value
		asin.mexglx		Inverse sine
		asinh.mexglx		Inverse hyperbolic sine
		atan2.mexglx		Four-quadrant inverse tangens
		atan.mexglx		Inverse tangens
		atanh.mexglx		Inverse hyperbolic tangens
		ceil.mexglx		Rounding towards +infinity
		cis.mexglx		Sine and cosine
		cis.m		Sine and cosine help
		cos.mexglx		Cosine
		cosh.mexglx		Hyperbolic cosine
		cot.m		Cotangens
		coth.m		Hypberbolic cotangens
		exp.mexglx		Exponential
		fix.mexglx		Rounding towards zero
		floor.mexglx		Rounding towards -infinity
		log2.mexglx		Binary logarithm
		log10.mexglx		Decimal logarithm
		log.mexglx		Natural logarithm
		mod.mexglx		Signed modulus
		pow2.mexglx		Scaling
		rem.mexglx		Signed remainder
		round.mexglx		Rounding to nearest
		sign.mexglx		Signum
		sin.mexglx		Sine
		sinh.mexglx		Hyperbolic sine
		sqrt.mexglx		Square root
		tan.mexglx		Tangens
		tanh.mexglx		Hyperbolic tangens

Warranty

Any warranty is strictly refused. Don't rely on any financial or technical support in case of malfunction or damage.

Comments are welcome. I will try to track reported problems and fix bugs.

History

April 23, 2004

Initial release

August 28, 2004

Service release thanks to a bug reported by Tom Minka in exp(matrix): the output was NaN for infinite input.

This bug fix made me think about affine inputs. They are now all handled as particular values for two reasons:

1. The output is well defined. In cases with more than one possible solution, the function limit towards that value has been used.
2. The performance does not degreade but increases considerably (table look-up instead of calculation). Any floating-point operation producing an affine result tries to throw an exception. Even if the exception is masked as within MATLAB, the processor calls up an internal assist slowing down the computation to about 10%-20% of normal performance.

Download

Downloading these files, you accept the copyright terms.

• Double class for MATLAB R13 or newer
  Digital signatures

Trademarks

MATLAB is a registered trademark of The MathWorks, Inc. Linux is a registered trademark of Linus Torvalds. Pentium II is a registered trademark of Intel Corporation. Other product or brand names are trademarks or registered trademarks of their respective holders.