• Introduction
• Example
• Comments
• Pitfalls
• Documents

Introduction

This page introduces floating-point assembler programming for MATLAB. It shows how to provide simple but performant routines. The source code uses the Netwide Assembler syntax. This assembler is open source and available for download at:

http://nasm.sourceforge.net/

Refer also to the Intel 32bit architecture IA-32 instruction set reference.

Floating-point unit

The Intel FPU's manage a stack of eight floating-point registers. These registers are 80bit long and use the temporary real format with a 64bit mantissa, a 15bit exponent and a sign bit. A control word defines the calculation mode. Of particular interest are:

1. Floating-point precision

   single
double (MATLAB)
   real (default)

2. Rounding mode

   chop towards zero
   round towards -infinity
   round towards +infinity
   round to nearest or even (default)

A status word flags the condition codes as for the integer unit. A tag word keeps track of register use and flags special values. The control and status word are accessible by particular assembler instructions, the tag word isn't.

Floating-point instructions

All floating-point operations imply the stack top register st0. Two-operand instructions use st0 either as destination (first operand, then result) or source (second operand). Single-operand instructions use it as source or destination. Figure 1 shows an example that writes in C as:

real st1=1.0;   // load operands
real st0=pi;
st0*=2.0^st1;   // scale pi
st1+=st0;
st1=sqrt(st1);
r=st1;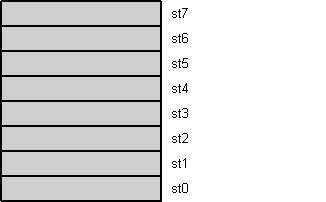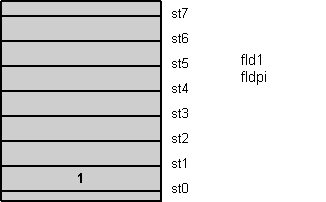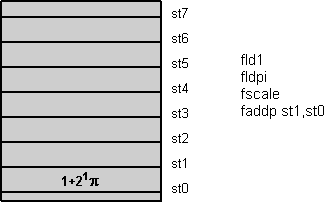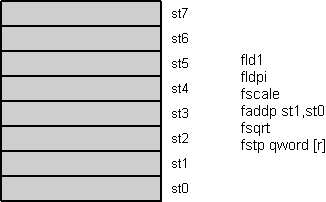

Figure 1: Floating-point register stack animation

All load instructions push the value onto the stack top. A push first decrements the stack top pointer, shown in figure 1 as register roll-up, and then loads the stack top st0 with the value. Store instructions work reversely. They first store the stack top value and then (optionally) increment the stack top pointer, shown as roll-down in figure 1.

Using the fdecstp and fincstp instructions, the stack top pointer can be decremented respectively incremented to roll another register on top. Use fxch st to swap st0 with st. Arrange the instructions carefully to avoid most of these 'no operations'.

Example

This example shows the assembler source for the vector length function vabs:

[segment .text]                   [Segments]
global	_fvabs


;void fvabs(double* oPr, const double* vPr,
;           const double* vPi, int n)
;
_fvabs: mov ecx,[esp+16]    ; n
        push ebx                  [Prologue]
        sub ecx,byte 1
       js       .0
        fninit                    [Reset]
        mov ebx,[esp+16]    ; vPi
        mov eax,[esp+12]    ; vPr
        test ebx,ebx              [Order]
        mov edx,[esp+8]     ; oPr
       jz       .2
.1:     fld qword [eax]           [Group]
        fmul st0,st0
        fld qword [ebx]
        fmul st0,st0
        add edx,byte 8
        faddp st1,st0       ; |x|^2
        fld qword [eax+8]         [Unroll]
        fmul st0,st0
        faddp st1,st0
        fld qword [ebx+8]
        fmul st0,st0
        faddp st1,st0       ; |y|^2
        fld qword [eax+16]        [Unroll]
        fmul st0,st0
        add eax,byte 24           [Alternate]
        faddp st1,st0
        fld qword [ebx+16]
        fmul st0,st0
        add ebx,byte 24           [Update]
        faddp st1,st0       ; |z|^2
        sub ecx,byte 1            [Count]
        fsqrt
        fstp qword [edx-8]  ; |v|
       jns      .1
.0:     pop ebx                   [Epilogue]
       retn
.2:     fld qword [eax]     ; real
        fmul st0,st0
        fld qword [eax+8]
        fmul st0,st0
        add edx,byte 8
        faddp st1,st0
        fld qword [eax+16]
        fmul st0,st0
        add eax,byte 24
        faddp st1,st0
        sub ecx,byte 1
        fsqrt
        fstp qword [edx-8]
       jns      .2
        pop ebx
       retn

Comments

[Segments]

Place assembler instructions in .code and data in .data segments. Align data elements on address boundaries that are an integer multiple of the element size.

[Prologue]

Preserve the contents of the following processor registers:

• Address registers: ebx, ebp, edi, esi
• Segment registers: cs, ds, es, fs, gs, ss

Don't create a stack frame if it isn't needed. But be aware of the latency after each push or pop instruction if followed by a memory access via the stack pointer esp.

[Reset]

MATLAB sets the precision to double (53bit mantissa). If you would like to use the full 64bit mantissa, you can either load the control word or initialize the floating-point unit. Initialization also resets all floating-point registers to empty.

[Order]

Sequentially access memory - either up or down - to profit from cache line reads. Interleave loads with subsequent calculations. These integer operations are executed during the initialization of the floating-point processor. Therefore, they take virtually no extra processing time.

[Group]

Bin loads and stores into groups to decrease the number of bus transfer alternations and to keep cache respectively memory transfer bandwidth high.

[Unroll]

Unroll loops with fixed but little number of repetitions. In this example, an inner loop over the three vector components (x,y,z) was unrolled into a single instruction sequence, thus eliminating a loop counter and conditional jumps.

[Alternate]

To maximize parallel execution, insert integer operations in between floating-point instructions.

[Update]

Minimize the number of register updates used as address pointers. Frequent modifications introduce additional latencies because subsequent address calculations need to wait on completion of the update instruction.

[Count]

Decrement the counter as early as possible. For this reason, the result pointer edx was updated well in advance.

[Epilogue]

Clean up floating-point registers if necessary. Restore the contents of the registers mentioned in the prologue.

Pitfalls

Heavy impact

• Avoid in any case a roll-over of the floating-point register stack.

  The floating-point unit throws a stack-overflow exception whenever an application tries to push more than 8 values simultaneously on the register stack. Because exceptions use a lot of processing time, even if masked, they slow down the execution to less than 20% of normal speed.

  After computation, either clean up floating-point registers by popping all values no longer needed, or free them in reverse order with ffree st.

• Keep intermediate values in floating-point registers.

  As shown in the C-MEX wrapper performance hints, the system memory bus bandwidth is a fraction of the internal data throughput bandwidth. Excessively writing intermediate results wastes bus bandwidth, but also adds rounding errors. Even the throughput of the first and second level cache may reach their limits if most floating-point instructions imply a memory operand.

• Minimize the number of square roots and divisions.

  Remind that a multiplication is many times faster than a division. A square root fsqrt or division fdiv[r][p] std,sts involves a sequence of comparisons and subtractions executed in order. In contrast, a multiplication simultaneously shifts and adds the values - no need to iterate over all bits waiting on a comparison each time.

  If possible, avoid square roots and divisions. Replace multiple divisions by multiplications with the inverse.

  Example 1: Multiple divisions

          push ebx
          mov ecx,elements
          mov ebx,divisor
          sub ecx,byte 1       ; avoid 'dec'
          mov eax,dividends
         js       .0           ; rare case
          mov edx,quotients
          fld qword [ebx]      ; load once
          add edx,byte 8
  .1:     fld qword [eax+ecx*8]
          sub ecx,byte 1       ; count
          fdiv st0,st1         ; slow
          fstp qword [edx+ecx*8]
         jns      .1
          ffree st0            ; clean up
  .0:     pop ebx
  

  The following code will run up to ten times faster:

          push ebx
          mov ecx,elements
          mov ebx,divisor
          sub ecx,byte 1       ; avoid 'dec'
          mov eax,dividends
         js       .0           ; rare case
          fld1                 ; load +1.0
          mov edx,quotients
          fdiv qword [ebx]     ; divide once
          add edx,byte 8
  .1:     fld qword [eax+ecx*8]
          sub ecx,byte 1       ; count
          fmul st0,st1         ; multiply
          fstp qword [edx+ecx*8]
         jns      .1
          ffree st0            ; clean up
  .0:     pop ebx
  

  The load and store operations were arranged to maximize pipelined execution throughput. For example, while waiting for ecx to load, ebx is already prefetched.

Medium impact

• Avoid frequent conditional jumps.

  Modern processors all have branch prediction units to minimize the pipeline latency on conditional jumps. Nevertheless, jumps should be avoided because they consume prefetch and decoding bandwidth upon first load. Compute the condition as early as possible to maximize the chance of a correct branch prediction. Use backward conditional jumps for frequent cases (loops) and forward jumps for rare cases. Avoid the complex loop[n][z] instruction.

• Keep the loop counter in a register.

  Don't place the counter in memory, particularly if the loop turns over in a few processor clocks. The memory latency slows down the execution speed.

• Avoid decrements and increments.

  Replacing a decrement dec x of the loop counter by a subtraction sub x,byte 1 saves processing time. The decrement and increment instructions cannot be pipelined. They don't modify all flags and have to wait on completion of all preceding instructions before being executed.

Light impact

• Avoid frequent register swaps and stack rolls.

  On recent processors, register swaps fxch st and stack rolls fdecstp respectively fincstp don't consume processing time as long as their issue rate is low.

Documents

See also the Intel Pentium 4 instruction reference and performance tuning guidelines at:

http://developer.intel.com/design/Pentium4/documentation.htm