• Introduction
• Requirements
• Implementation details
• References
• Copyright
• Warranty
• History
• Download
• Trademarks

Introduction

The Hankel transform of order n (1) transforms rotationally symetric inputs in a computationally efficient manner. In particular, the Hankel transform of order 0 is equivalent to the two-dimensional Fourier transform of a rotationally symetric input. This package contains four implementations of the Hankel transform (1) and the inverse Hankel transform (2), respectively.

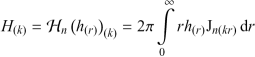	(1)
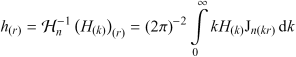	(2)

J_n is the Bessel function of the first kind of order n.

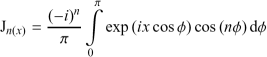(3)

Requirements

• MATLAB 6.0 or newer.

Implementation details

Hankel transform of order n: hat, ihat

The Hankel transform implements a direct integration of equation (1). The integration is performed as a matrix product of the integration kernel J_n with the integrand I = rhΔr.

(4)

The integrand is the product of the signal with the ring area between neighboring mid-points.

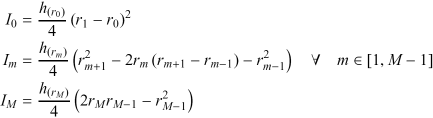(5)

The algorithm does not require any particular sampling at the exception of respecting Shannon's sampling condition. For the Hankel transform, the signal h and the kernel need to be resolved along the radius r. For the inverse transform, the spectrum H and the kernel need to be resolved along the spatial frequency k.

Hankel transform of order 0: ht, iht

This implementation is equivalent to the previous implementation for order 0. The integration of the Bessel function is performed a priori for obtaining the integration kernel more accurately. Hence, only the signal h need to be resolved along the radius r for the Hankel transform. For the inverse transform, only the spectrum H need to be resolved along the spatial frequency k.

For instance, the Hankel transform of a constant signal h = 1 up to a radius R is obtained with H = ht(h,R,k). This means that the signal needs a single sampling point, whereas the other functions request many points.

Quasi-discrete Hankel transform of integer order n: dht, idht

The quasi-discrete Hankel transform [1] is equivalent to the discrete Fourier transform algorithm. The transform uses a square, unitary matrix as integration kernel (7). The product of the kernel with a scaled signal (9) yields a scaled spectrum (8) and vice versa.

The sampling points are given by the roots z of the Bessel function J_n. The position and frequency sampling points are

(6)

where R is the maximum radius. The unitary integration kernel is then

(7)

and the scaled signal and spectrum are

	and		(8)
The forward and the inverse Hankel transform are then given by the matrix products
	and		(9)

Quasi fast Hankel transform of order n: fht, ifht

This implementation applies the Gardner transform [2] to the position and frequency variable r and k, respectively. The product kr gets the sum u + v in the transformed variables. Therefore, the Hankel transform turns into a convolution, which can be efficiently computed with Fourier transforms [3].

References

1. M. Guizar-Sicairos, J.C. Gutierrez-Vega, "Computation of quasi-discrete Hankel transforms of integer order for propagating optical wave fields," J. Opt. Soc. Am. A 21, 53-58 (2004).
2. D.G. Gardner, J.C. Gardner, G. Lausch, W.W. Meinke, "Method for the analysis of multi-component exponential decays," J. Chem. Phys. 31, 987 (1959).
3. A.E. Siegmann, "Quasi fast Hankel transform," Opt. Lett. 1, 13-15 (1977).

Copyright

This package is freeware. The author reserves the right to modify any of the contained files.

You are allowed to distribute it as long as you deliver the entire, original package for free.

Path		File		Description
/		dht.m		Quasi-discrete Hankel transform of integer order n
		dht.mat		Roots of Bessel functions of the first kind
		fht.m		Quasi fast Hankel transform of order n
		hat.m		Hankel transform of order n
		ht.m		Hankel transform of order 0
		idht.m		Inverse quasi-discrete Hankel transform of integer order n
		ifht.m		Inverse quasi fast Hankel transform of order n
		ihat.m		Inverse Hankel transform of order n
		iht.m		Inverse Hankel transform of order 0
		Readme.txt		Summary
private/		frdr.m		Integrand
		JnRoots.m		Roots of Bessel functions of the first kind

Warranty

Any warranty is strictly refused. Don't rely on any financial or technical support in case of malfunction or damage.

Comments are welcome. I will try to track reported problems and fix bugs.

History

December 13, 2006

Initial release.

April 10, 2007

Bug fix in FHT thanks to Mark W. Sprague.

July 29, 2009

Bug fix in DHT thanks to Nicolas Grisouard. Hankel transforms of order 1 or higher require to take care of the first root (zero) of the Bessel functions of the first kind when calculating the transformation kernel (avoid division by zero).

Download

Downloading these files, you accept the copyright terms.

• Hankel transforms for MATLAB 6.0 or newer
  Digital signature

Trademarks

MATLAB is a registered trademark of The MathWorks, Inc.